Electric resistance is a fundamental concept in electronics, and understanding it is key to understanding how circuits work. Think of electrical resistance as a kind of friction for electricity – just as friction slows down a moving object, resistance slows down the flow of electric current. In the image, it is shown that electrons scatter off atoms (black dots) in a resistive medium and do not move in a straight line, leading to more energy loss.
What is Electric Resistance?
In simple terms, electrical resistance is a measure of how much a material opposes the flow of electric current. When electricity flows through a conductor (like a copper wire), not all of it passes through easily – some of the energy is lost as heat due to the material’s resistance.
Resistance is measured in ohms (Ω), named after the German physicist Georg Simon Ohm. The higher the resistance, the harder it is for electricity to flow. Conversely, a lower resistance means that electricity can flow more easily.
Real-World Analogy: Water Flow
To better understand resistance, let’s compare it to something more tangible – water flowing through a pipe. Imagine you have two pipes: one wide and one narrow. Water flows easily through the wide pipe but struggles to get through the narrow one. In this analogy:
- Water Flow = Electric Current
- Pipe Width = Conductor’s Resistance
The narrower pipe (more resistance) restricts the flow of water (current), while the wider pipe (less resistance) allows more water to pass through easily.
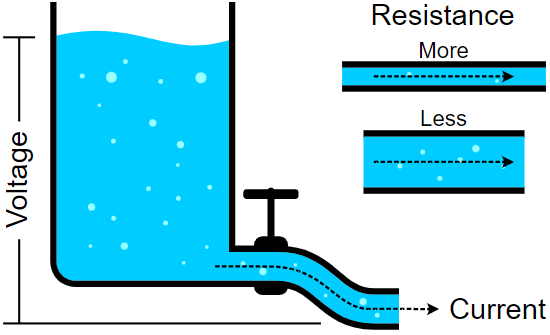
If the voltage is increased, more electric current will flow – an analogy to this is that the higher the water level in a tank, the more intense the flow will be through a pipe of the same diameter.
Why Does Resistance Matter?
Resistance plays a crucial role in determining how much current flows through a circuit. If you’re designing a circuit, you need to control the current to ensure that your components work correctly and safely.
For example, consider the simple act of turning on a light bulb. Inside the bulb is a thin wire called a filament, usually made of tungsten. This filament has the exact needed resistance, which causes it to heat up and glow when electricity passes through it, producing light. If the resistance were too high, the filament would not get hot enough to glow because not enough current could pass through it, and the bulb wouldn’t produce light. On the other hand, if the filament’s resistance is too low, too much current will pass through it, and the filament would burn out due to excessive heat.
Ohm’s Law: The Key Relationship
Ohm’s Law is a fundamental principle that relates voltage (U), current (I), and resistance (R) in a circuit. The law is expressed as:
I – Electric current in Ampere [A]
U – Voltage (potential difference) in Volt [V]
R – Electric resistance in Ohm [Ω]
This equation means that the electric current through a circuit is proportional to the applied voltage and inversely proportional to the circuit resistance. If you know any two of these values, you can calculate the third.
For example, if you have a resistor with a resistance of 10 ohms, and it is connected to a voltage source of 20 volts, the current through the resistor would be: I = U / R = 20 / 10 = 2A.
In another example, if you have a resistor with a resistance of 10 ohms and a current of 2 amperes flows through it, the voltage across the resistor would be: U = I * R = 2 * 10 = 20V.
Resistance of wire and resistivity of material
So now we know what Ohm’s Law is and how we can calculate the current through a circuit if we know the resistance and applied voltage. But how can we calculate the resistance of a basic component, like a simple wire? A wire is essentially just a material, such as copper or aluminum, shaped into a wire-like form (either cylindrical or square).
Copper and aluminum, for example, are basic elements in nature, and one of their specific properties is electrical resistivity. Resistivity is commonly represented by the Greek letter ρ (rho). The SI unit of electrical resistivity is the ohm-meter (Ω·m).
For instance, if a solid cube with a volume of 1 cubic meter has electrical contacts on two opposite faces, and the measured resistance between these contacts is 1 ohm, then the material’s resistivity is 1 ohm-meter.
| MATERIAL | RESISTIVITY ρ (rho) AT 20°c |
|---|---|
Silver | 1.59×10−8 |
| Copper | 1.68×10−8 |
| Annealed copper | 1.72×10−8 |
| Gold | 2.44×10−8 |
| Aluminium | 2.65×10−8 |
| Brass (5% Zn) | 3.00×10−8 |
| Calcium | 3.36×10−8 |
| Rhodium | 4.33×10−8 |
| Tungsten | 5.60×10−8 |
| Zinc | 5.90×10−8 |
| Brass (30% Zn) | 5.99×10−8 |
| Cobalt | 6.24×10−8 |
| Nickel | 6.99×10−8 |
| Ruthenium | 7.10×10−8 |
| Lithium | 9.28×10−8 |
| Iron | 9.70×10−8 |
| Platinum | 10.6×10−8 |
| Tin | 10.9×10−8 |
| Phosphor Bronze (0.2% P / 5% Sn) | 11.2×10−8 |
| Gallium | 14.0×10−8 |
| Niobium | 14.0×10−8 |
| Carbon steel (1010) | 14.3×10−8 |
| Lead | 22.0×10−8 |
| Galinstan | 28.9×10−8 |
| Titanium | 42.0×10−8 |
| Grain oriented electrical steel | 46.0×10−8 |
| Manganin | 48.2×10−8 |
| Constantan | 49.0×10−8 |
| Stainless steel | 69.0×10−8 |
| Mercury | 98.0×10−8 |
| Nichrome | 110×10−8 |
| Bismuth | 129×10−8 |
| Manganese | 144×10−8 |
| Plutonium (0 °C) | 146×10−8 |
| Carbon (graphite) – parallel to basal plane | 250×10−8 to 500×10−8 |
| Carbon (amorphous) | 0.5×10−3 to 0.8×10−3 |
| Carbon (graphite) – perpendicular to basal plane | 3.0×10−3 |
| Sea water | 2.1×10−1 |
| Swimming pool water | 3.3×10−1 to 4.0×10−1 |
| Germanium | 4.6×10−1 |
| Drinking water | 2×101 to 2×103 |
| Wood (damp) | 103 to 104 |
| Silicon | 2.3×103 |
| Deionized water | 1.8×105 |
| Air | 109 to 1015 |
| Ultrapure water | 1.82×109 |
| Glass | 1011 to 1015 |
| Carbon (diamond) | 1012 |
| Hard rubber | 1013 |
| Wood (oven dry) | 1014 to 1016 |
| Sulfur | 1015 |
| Fused quartz | 7.5×1017 |
| PET | 1021 |
| PTFE (teflon) | 1023 to 1025 |
We know that a longer conductor creates more resistance to current flow, and similarly, a thinner conductor also creates more resistance to current flow (just as a thin hose carries less water). Finally, from the table above, we can see that some materials naturally support current flow easily, while others restrict it (this is analogous to a brand new pipe allowing water to flow freely versus an old one with debris and residue that restricts water flow).
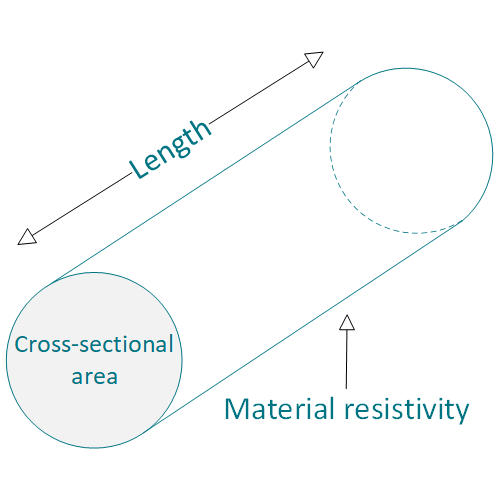
All of this makes it possible to create a universal formula for calculating the resistance of an object if we know its dimensions and material electric resistivity:
R – electric resistance in Ohms [Ω]
ρ – material electric resistivity in Ohm meters [Ωm]
L – length of material in meters [m]
A – cross sectional area of material in square meters [m2]

When we talk about conductors, we know that these materials have very low resistance to electric current flow and can easy conduct electric current. The opposite situation occurs when a material has extremely high resistance to electric current flow, and in that case, the material is called an insulator.
By understanding a material’s electrical resistivity and how resistance depends on its length and cross-sectional area, we can design specific electronic components with precisely the resistance we need. These components are called resistors.
Conclusion
Electrical resistance is a simple yet powerful concept that underpins much of what happens in electronics. Whether you’re powering a light bulb or charging your phone, understanding how resistance works helps you see the hidden complexities in the devices you use every day. As you continue learning about electronics, keep Ohm’s Law and the water flow analogy in mind — they’ll help you make sense of more advanced topics down the road.


Leave a Reply